之前介绍了堆排序和归并排序,今天来说说快速排序。快速排序是应用较多的一种排序方法。
各算法平均排序时间:
数据是随机整数,时间单位是秒。(网上的数据,仅供参考)
数据规模 快速排序 归并排序 希尔排序 堆排序
1000万 0.75 1.22 1.77 3.57
5000万 3.78 6.29 9.48 26.54
1亿 7.65 13.06 18.79 61.31
堆排序是最差的,这是算法硬伤,没办法的。因为每次取一个最大值和堆底部的数据(记为X)交换,重新筛选堆,把堆顶的X调整到位,有很大可能是依旧调整到堆的底部(堆的底部X显然是比较小的数,才会在底部),然后再次和堆顶最大值交换,再调整下来。从上面看出,堆排序做了许多无用功。
快速排序原理:
快速排序法是采用递归的方式对待排序的数列进行若干次的操作,每次操作使得被操作的数列部分以某个元素为分界值分成两部分,一部分小于该分界值,另一部分大于该分界值.该分界值一般被称为"枢轴". 一般先以左边第一个数作为分界值,将数列按该分界值分成左右两部分,左边部分小于该分界值,右边部分大于该分界值,然后再对左右两部分做重复的操作,直到最后完成排序。
以数列 14,11,25,37,9,28 为例,详细描述执行一趟快速排序的算法:
1,选择待排序数列的枢轴,一般以数列的首元素作为枢轴.此数列中,我们选择首元素14作为枢轴,nPivot = 14.
2,设定两个指针 i 和 j ,分别指向数列的首元素和尾元素. i 指向首元素14, j 指向尾元素28.示意图如下:

3,向前移动尾指针 j ,使其指向从数列尾部算起首个小于枢轴(即14)的元素,并将该元素置换到头指针 i 指向的位置._nArray[i] =_nArray[j].示意图如下:

首次执行该操作时 i 指针指向处的值实际上就是枢轴的值,此处的操作可以理解为 i 指针指向处的值已在之前被置换到枢轴中,此时, i 指向处已经是一个空位,在此时用找到的小于枢轴的元素填在此处.
4,向后移动头指针 i ,使其指向从数列头部算起首个大于枢轴(即14)的元素,并将该元素置换到尾指针 j 指向的位置._nArray[j] =_nArray[i].示意图如下:
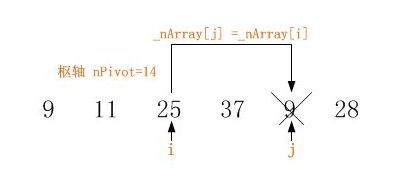
此处同样可以理解为 j 指针指向处的值已在上一步操作中置换了出去. j 处已是一个空位.
5,如此重复执行步骤3和步骤4,直至 i==j 时结束该循环.
6,退出了该循环后, i 与 j 必定指向同一位置.在该位置的前部元素,其值均小于枢轴.而在该位置的后部元素,其值均大于枢轴.显而易见,此时 i 和 j 同时指向的位置就应该是枢轴的"新家"._nArray[i]=nPivot.如下图:

至此,一趟排序结束.待排序数列的首元素将该数列分成了比其小和比其大的两部分.如下图:
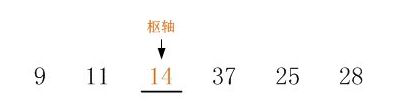
接着,我们对这一大一小两部分子数列执行相同的排序操作.
如此"递归",直至对整个数列完成排序操作。
C#实现代码
using System;using System.Collections.Generic;using System.Linq;using System.Text;using System.Threading.Tasks;namespace QuickSort{ class QuickSort { static void Main(string[] args) { //声明数据进行相应的测试 int[] myArray = new int[] { 45, 36, 18, 53, 72, 30, 48, 93, 15, 36 }; //myArray = new int[] { 3, 4, 5, 1}; int lowIndex = 0; //数组的起始位置(从0开始) int highIndex = myArray.Length - 1; //数组的终止位置 //快速排序 QuickSortFunction(myArray, lowIndex, highIndex); //输出排完之后的数组 for (int i = 0; i < myArray.Length; i++) { Console.WriteLine(myArray[i].ToString()); } } //快速排序(目标数组,数组的起始位置,数组的终止位置) private static void QuickSortFunction(int[] array, int low, int high) { int keyValuePosition; //记录关键值的下标 //当传递的目标数组含有两个以上的元素时,进行递归调用。(即:当传递的目标数组只含有一个元素时,此趟排序结束) if (low < high) { keyValuePosition = keyValuePositionFunction(array, low, high); //获取关键值的下标(快排的核心) QuickSortFunction(array, low, keyValuePosition - 1); //递归调用,快排划分出来的左区间 QuickSortFunction(array, keyValuePosition + 1, high); //递归调用,快排划分出来的右区间 } } //快速排序的核心部分:确定关键值在数组中的位置,以此将数组划分成左右两区间,关键值游离在外。(返回关键值应在数组中的下标) private static int keyValuePositionFunction(int[] array, int low, int high) { int leftIndex = low; //记录目标数组的起始位置(后续动态的左侧下标) int rightIndex = high; //记录目标数组的结束位置(后续动态的右侧下标) int keyValue = array[low]; //数组的第一个元素作为关键值 int temp; //当 (左侧动态下标 == 右侧动态下标) 时跳出循环 while (leftIndex < rightIndex) { //右侧动态下标逐渐减小,直至找到小于或等于keyValue的下标,然后把他交换到左端 while (leftIndex < rightIndex && array[rightIndex] >= keyValue) { rightIndex--; } temp = array[rightIndex]; array[rightIndex] = array[leftIndex]; array[leftIndex] = temp; //左侧动态下标逐渐增加,直至找到大于keyValue的下标,然后交换他到右端 while (leftIndex < rightIndex && array[leftIndex] <= keyValue) { leftIndex++; } temp = array[leftIndex]; array[leftIndex] = array[rightIndex]; array[rightIndex] = temp; } return leftIndex; } }}